ブログをやめてワープレに引っ越した
https://drroot.page/
ので今後このブログは更新を停止し置物と化す
ちなみに引っ越し理由はただの気まぐれ
低価格高音質なバイノーラルマイクを自作した(完成版)
自作マイク関連の記事は過去何度か書いてきたが、現時点ではこの記事の内容が決定版なので他のは見なくていい。
概要

最近なんやかんや流行りになりつつあるダミヘで音フェチ録るやつだ。
マイクアンプ(XLRコネクタ、ファンタム不要)を既に持っている事が前提だが、それさえあればいい音が録れる。
ちなみにマイクアンプといってもオーディオインターフェースにはたいてい標準で付いており、例えばZOOM H4なんかでもXLR入力が2個付いてるので問題なく使えるぞ。
電気回路
マイクはC9767の3線式改造で高音質を実現。9V電池をマイクとオペアンプに与え、4.7倍の増幅をかけてXLRのHOT/COLDに与えるシンプルな構成だ。
回路図は電子工作に明るくない人がなるべく簡単にはんだ付けできるよう、秋月のブレッドボード型基板を採用した。
文字あり配線図↓

文字なし配線図↓

回路図↓

電源に挿れてる470u書き忘れた
回路図では1ch分しか書いてないが、赤枠の電源部分以外を2つ分実装してLR2ch分にしている。
3線マイク改造やオペアンプ回路の理論的な部分は他のサイト様で既出だが、ファンタム電源を使わずバッテリー駆動に割り切ることで音フェチを楽しむに耐えうるS/N比を出せた。
オペアンプを使ってバランス出力を作ることで、A/Iなりマイクアンプなりの性能を素直に活かす構成だ。結局余計な味付けをせずあるものを最大限活用する方が美味い。
配線図の見方だが、赤色は上を配線、青色は下側を配線、真ん中の2つのソケットはオペアンプを挿す8ピンだが、オペアンプ直挿しでも良い。
コンデンサは全て無極性のMUSE電解コンデンサを採用。理由は何か光ってて見た目がカッコいいからだ。音質とかは一切知らん(積層セラミック以外どれも違いがわからん)。
抵抗は余ってた在庫を採用、オペアンプはNJM4580DDで全て揃えても数百円(秋月電子)。
ブレボ基板は英字と数字が書いてあるので、それを参考にパーツを挿していけば簡単にコピーが作れると思う。
出力のXLRコネクタは2パターンの取り付け方がある。
マイクケーブルも作ってしまう方法と、マイクケーブルは別途用意することにして、筐体にはXLRのコネクタをとりつける方式だ。
自分が作ったのはケーブルを直接生やす方式だが、利便性を考えるとコネクタを取り付けたほうが良い。
3線式改造については過去の記事を参照。
もっと真面目にパナ改を作った - 落胆がらくた街
筐体設計
電気回路が出来たら次はマイクの取り付けをする。ダミーヘッド的な構造を作成する必要があるので、10cm立方体のアクリルボックスと鍼灸練習用の耳型を購入。各1000円也。
はこ
みみ
今回はMDF材で耳型を補強するように固定したが、アクリルボックスに接着剤で直付けすればよかったと思った。
耳型は予めマイクを通す穴を開ける必要があるが、RCAジャックの内径がちょうど10ミリなのでこれでくり抜くとやりやすい。
アクリルボックスの裏側には、XLRコネクタとスイッチを取り付ける。
つかいかた
余ったMDF材耳に突っ込んでこすったりするとこういう音が録れる。
www.youtube.com
メイキング
動画近日あげます
パーツリスト(新規で買い揃える場合)
秋月電子。送料全国どこでも500円。
・コンデンサ…1uF(3つ)、4.7uF(6つ)、470uF(1つ)
・ブレボ基板
・8ピンソケット
・NJM4580DD(2つ)
・トグルスイッチ
・9V電池ソケット
・LED
・配線用ケーブル
アマゾン。送料無料~100円くらい。買ってから着くまで二週間とかする。
・はこ
・みみ
・抵抗20本30種セット
サウンドハウス。1000円以上で送料無料なのでなんとかしよう。
・コネクタ(2つ)
・↑の奴専用ねじ(4つ)
・マイクケーブル(2本)
直挿しでやる場合代わりにコネクタとマイクケーブル単体をサウンドハウスで買えばいいと思う。
あとA/I持ってねぇやつはベリンガー様に貢いどけ
バイノーラル録音システムを自作する Part3:アンプ実用編
とりあえず普通のマイクシステムとして使う例
バイノーラルかどうかは電気的には関係ないので、とりあえず「モノラルのECMアンプ」として使ってみる。
アンプの入力部は標準的なステレオミニプラグ(L=ドレイン、R=ソース、GND=GND)を採用したので、マイク側は三線改造した上で百均のイヤホン何かに繋いでおく。
すっかり保留にしてきたマイクの三線改造だが、今回はEM158を例に挙げる。
EM158の改造に関しては下の記事が詳しい。
1913 :プリモ EM-158三線式改造法(改良版) | ShinさんのPA工作室
一点補足すると、ミニルーターは必須で無い。
アクリル板なんかを加工するのに使うプラカッターなどで削っていけば手動でも十分加工できるぞ。

で、このEM158は、秋月で手に入る他のEMC(WM61やその互換品、C9767等)と違い、有能ポイントが一つある。
マイクカプセルのケースにハンダが乗る事だ。
その為下記画像のような、ドレインとソースだけ配線してGNDはケースにくっつけるという荒業ができる。

ケースは標準的なRCAジャックだ。100均のイヤホンなりステレオ延長ケーブルなりを捌いて予めマイクに繋いだあとジャックの穴を通し、
RCAジャックの口のところにEM158がぴったり乗っかるのでケースをはんだ付けすれば出来上がり。
困難なマイクへのはんだ付けも、GND一本分ケチれるのでかなり楽に済む。

なおバイノーラルマイクであればパネル取り付け式のRCAジャックを使うと便利。
つかってみる
最近こういう事をして遊んでいるので、よかったら見てみてね。
www.youtube.com
5月以降の動画は上記のマイクで録音しているよ。
バイノーラル録音システムを自作する Part2:ECMアンプ回路
2019 8 21 追記
エレクトレットコンデンサマイク改造についてのまとめ | 落胆がらくた工務店
更に改善した。コッチヲ見ロォ!
ECMアンプについて
目的:3線改造したECMを入力に受け、オーディオインターフェースのXLRに出力できるアンプを作る
ECMの3線改造については後述
何が便利なのか:秋月とかで売ってるECMを高音質でPCに取り込める
完成像


アルミケースは偶々もらったものを使ったが、買うと1000円前後するので、既成品から剥ぐなり100均で似たようなもの探すなりしてもいい。
金属製でないと電磁波ノイズ直撃で最悪の場合AMラジオ拾ったりするので、どんな安物でもいいから金属ケースで覆う事を推奨。
コネクタやスイッチ類は手元にあったものを流用したが、これもジャンクから引っ剥がしたりしたモノで大抵事足りる。
XLRコネクタだけはケーブル共々サウンドハウスが安く売ってくれるが、別に直接基盤からケーブルを生やしても問題無い。
機能ブロック図

発想は至ってシンプルで、TPS7Aで作った綺麗な8Vをマイクとオペアンプに供給し信号を増幅するだけ。
回路図

オペアンプ回路を知っている人であれば教科書的な回路に見えると思う(というか自分がその程度の回路しかつくれない)。
ECMソースフォロワ→非反転増幅しつつコールド出力→反転増幅1倍でホット出力のバランス構成。
以下、各素子の詳細と定数の理由。
R1…マイク内蔵のFETと共にソースフォロワを形成する。内蔵FETの詳細はデータがないので470~10kくらいでいい感じに音が取れる数値を総当たりする。
わんぽいんと:ここをボリュームにして、繋ぐマイクに合わせて手動でソース抵抗を変えられるようにするのもアリかも?
C1…カップリングコンデンサ。R10と合わせてHPFを形成する。0.22u~10u程度を推奨。あまりデカいと放電モード時R1で引き抜けなくなる。
R2…VR1と合わせて、オペアンプの帰還抵抗を形成する。VR1が0の時帰還抵抗が0になるのを防ぐため挿入。
R3…オペアンプの帰還抵抗の一部。非反転増幅回路なので、全体ゲインは(R1+VR1)/R2。
C2…オペアンプの直流に対する利得を1倍にする為挿入。そこそこ大きくないと低域が落ちる。4.7u~推奨。
C3…カップリングコンデンサ。C1以上なら音質に影響ないはず。R4とHPFを形成するので、本当はC1=C3、R4=R10が望ましいが誤差。
C4…うっかりファンタム電源をONにしちゃった時の保護用コンデンサ。耐圧50V以上、両極性。一応信号をカップリングするのでC3の3倍程度取る。
R4…C3、C4放電用兼HPF形成。
R5…反転増幅回路の入力抵抗。ざっくり計算だが10kより少ないと周波数特性が落ちこれより大きいとノイズに弱くなる。
R6…反転増幅回路の帰還抵抗。R5とR6は高精度の抵抗を用いぴったり1倍に近づける事を推奨。
C5…カップリングコンデンサ。両極性、耐圧50V以上。容量はそこそこ大きけりゃあとは適当。今回はC4と同じに。
R7…C5放電用兼HPF。
R8…バイアス電圧生成用。大きいと高インピーダンスの影響で、小さいと熱雑音の影響で音質に影響する。1k~10kが妥当?
R9…同上。
C6…バイアス電圧の直流安定を得るため挿入。10uはでかすぎる気がするけどまあいいか!最悪無くても良い。
R10…バイアス電圧を信号に乗せるための抵抗。交流的には接地されている為C1とHPFを形成する。
R11…同上。ちなみにR4、R7、R10、R11は同じ値が望ましい。
ちなみにオペアンプはNJM4580DDを採用。だって安いんだもん。
あとはユニバーサル基板にざっくりはんだ付けして完成。一点アース?知らんな!w
バイノーラル録音システムを自作する Part1:概要
バイノーラル録音したい。音フェチやりたい。でも金が無い*1。
というわけで廉価かつ高音質な録音環境を自作した。なんやかんや大規模になってしまったので数パートに分割して書く。
本記事は全体像の紹介だ。
説明!!
制作の目的を以下に挙げる。
- バイノーラル録音に耐える音質である
- 歪率が許容できる範囲内である
- S/N比がマイクカプセル本来の性能にできるだけ近い
- 最終的な材料費を3000円程度とする
- 手元にあるオーディオインターフェースがXLR入力×2を持ってるので、出力はこれにつなぐ
なお、昔イヤホン型の小型バイノーラルマイクを作ったが、今回はECMソースフォロワ改造+外部電源方式+オペアンプ使用のリッチな方式だ。
机の上でパソコンに繋いで録音するならこちらの方が遥かにいい音が録れる。当時自分が未熟だったのもあり、今だとこっちがよっぽどお勧めだ。
設計
まず最初に最終型がどうなったかを書く。
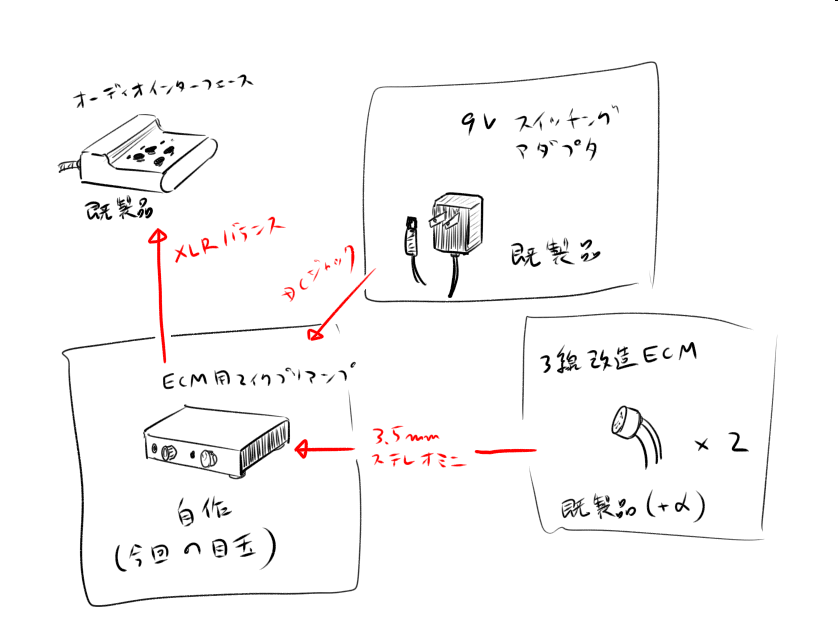
マイクアンプは「3線式ECMだけを対象にする」と決め打ってしまい、マイクの交換がしやすいようステレオミニプラグで接続する。
ここはマイクとアンプを3本の線で繋げられれば何でもいいのだが、ステレオミニプラグは100均で買ったイヤホンを捌けば手に入るのがポイント。
アンプ本体は当初A/Iからのファンタム駆動を考えていたが上手くできなかったので、秋月9Vアダプタ+TPS7A4700というDC-DCコンバータを採用した。
TPS7Aというのは本システム最高のお値段がする財力の暴力で、こいつだけで1100円する。後述するがこれを9V電池に置き換えると10回交換するまでは安く済む。
スイッチングアダプタは秋月で買った9Vのものを使ったが、レギュレータで電圧を落とす都合上9~12Vの製品であれば適当なものを流用してもいい。
あとはマイクから3線を引き出してステレオプラグを生やし、アンプ→A/Iと繋げば音が取り込めるわけだ。
秋月ECMはもちろんの事、既成品の安物マイクもECMが使われてさえいればちょっとした改造でそれなりの音質に化ける。
例えばこれ。→iBUFFALO マイクロフォン ミニクリップ ブラック BSHSM03BK バッファロー
1レッドブル強で買えてしまうが、バラして3線改造→自作アンプに接続とする事でそれなりの音質が叩き出せてしまう。
つまりこのアンプは「ECM専用マイクプリ」と言える。
BM700(or BM800)の動作について考えてみた
この記事は概ね下記ページの翻訳である。
Basic FET Circuits for Mics
BM700って何
大体1500円くらいで買える中華安物マイク。BM800もマイナーチェンジらしく回路は同一らしい。
国内外を問わず「安物マイクだが改造すると音が良くなる」という事で、一部のキモ・オタクから人気の製品だ。
ところが回路の意味がイマイチ分からず、結局日本語でそれらしい解説をしてる記事がなかったので備忘録がてら記事にする。
そもそもの課題は何か
何故たかだかマイク一つにこんな苦労をするかと言うと、「一般に使われるマイクプリアンプは最近主流のエレクトレットコンデンサマイク(以下ECM)用にできてない」からだ。
マイクには「ダイナミック」「コンデンサ」「エレクトレットコンデンサ」の3種類が存在し、入力機器側もそれぞれ「Hi-Z入力」「ファンタムありのXLR」「プラグインパワー」と対応している。
ECMは元々廉価で小規模なプラグインパワーでの動作を想定されており、うっかり高音質なECMが時代の流れでできちゃったもんだから、
「本来コンデンサマイク用のファンタム電源しか無い録音機材業界で、なんとかECMを駆動させたい」という需要ができたわけだ。
極端な話、高品質なプラグインパワー端子がオーディオインターフェースに乗っかっていれば、こんな悩みも無いのだが、そういうわけにはいかんので「ECM←→XLRファンタム変換回路」が必要になる。
今回扱う回路もそんな回路の一種だ。
Shoeps Circuit
まずBM700の回路について考える前に、Shoeps回路と呼ばれる、XLR接続・ファンタム電源印加でECMを駆動させる回路について考えよう。
先程の翻訳元のページから、下記回路図を拝借した。これがShoeps回路の基礎である。

大まかな流れとしては、
0.XLRからやってきた48Vから上手いこと電流を引き出す(赤枠)
1.マイクカプセルの出力はカスなので初段増幅(青枠)
2.XLRは2つの端子に逆相で信号を乗せないといけないので信号を変換(緑枠の部分)
といった感じ。で、一番わけがわかんねぇのは緑の部分、PNPトランジスタが2つ並んでいるやつだ。
共通部分から電流を取り出すところや、逆相を増幅するところは一見差動増幅回路のようだが、これは差動増幅回路ではない。
なんなら厳密なバランス回路でもない。多分。
いざBM800へ
正直BM800の回路に関しては、下記ページが最もわかりやすく充実しているので、最早今更言うことがない。
エレクトレット・コンデンサ・マイクBM-800の改良
若干補足すると、回路の全体像は概ねShoeps回路そのもの。ただし電源の特性を改善する為ツェナー+レギュレータ回路を採用している。
またHOT・COLDの直後に22nFと47Ωの抵抗がぶっ刺さっているが、これはノイズを改善するためのものらしい。
上記ページからリンクが貼られているが、防振など物理的な改善に関してはいつものパナ改の方が記事を上げている。
1603 :Amazonの超激安コンデンサマイクが高級機に変身する改造(第1編) | ShinさんのPA工作室
今後の課題
秋月で売ってるイサハヤのPch JfetでPNPトランジスタ置き換えて、自前のShoeps回路組んでみたい。でもまだ回路理解しきれてない。
